量子計算基礎 - 從單量子位到多量子位系統

大一下去修了一門量子計算的課，前面的概念跟線性代數有滿多相似的地方，後半部分才真正開始講量子演算法。

量子計算基礎簡介

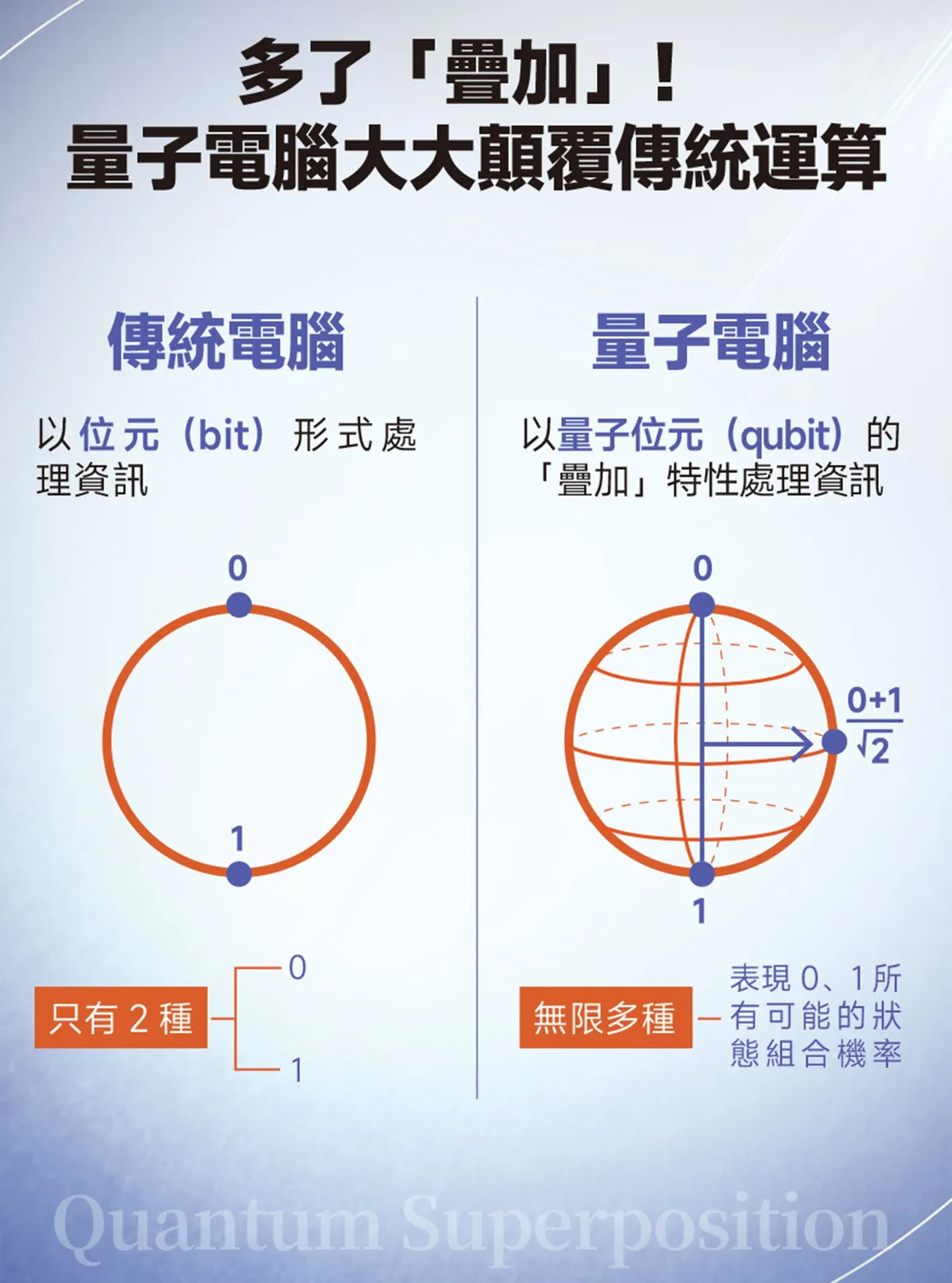
量子電腦與傳統電腦的差別，在於傳統電腦儲存資訊的最小單位是位元（bit），量子電腦則是使用量子位元（qubit）。位元可以存在一種狀態，1 或是 0。量子位元特別的地方是，它在一個時間，可以同時是 1 也是 0。

量子在通訊上有很高的安全性，利用量子力學原理，能夠在兩方之間安全地分發加密密鑰。任何試圖竊聽的行為都會擾亂量子態，被接收方檢測到。

過去超大整數的質因數分解，即使傳統超級電腦的運算能力也無法在短時間破解。不過，量子演算法（Shor’s Algorithm，可解質因數分解）能在合理時間內完成破解，會顛覆現在 RSA 等加密算法。

Classical v.s. Quantum

拆解質數

現在有個數字 N = f₁ × f₂，由 f₁, f₂ 兩個很大的質數構成。破解 RSA 的核心，就是從 N 找出 f₁ 和 f₂。

想要找到 N 的因數，只要不斷給定 g，透過 Euclid’s Algorithm（歐幾里得演算法，又稱輾轉相除法）快速計算判斷，當 g 使得公因數 gcd (N,g) = a > 1 時，對於 RSA 來說就已經結束了。

但要找到 g 可以滿足上述條件其實並不容易，事實上真的只能一個一個猜 g 是多少。不過，我們可以將這個隨機猜測的數字 g 轉換成很有可能滿足條件的 g^p/2 ± 1。

為什麼是 g^p/2 ± 1 ？

若給定兩個數 A, B，且 gcd (A,B) = 1，則存在一個正整數 p 使得 A^p = m ⋅ B + 1，其中 m 為某個整數（根據歐拉定理）。

舉兩個例子來說：

Ex1

給定 (A,B) = (7,15)，則：

Ex2

給定 (A,B) = (42,13)，則：

因此，m ⋅ B = A^p − 1 = (A^p/2+1)(A^p/2−1)

將機會不大的數字 g 轉換成很有可能的g^p/2 ± 1，只要找到這樣的p就好（p要是偶數才能真正拆解喔！）

Classical

我們用個例子來想，要用傳統電腦找到一個 p 使得 42^p = m × 13 + 1，可能會從 p = 1, 2, 3, … 開始一個一個慢慢代入判斷，但如果現在給定 g^p = m × N + 1 的 g 和 N 都很大呢？

對傳統電腦來說，就真的只能一個一個數字慢慢算，直到找到答案為止，這也就是為什麼現在能夠這麼廣泛地使用 RSA 加密。但是對量子電腦來說就不太一樣了……

Quantum

用量子來計算的好處是因為有疊加態（superposition）。

我們可以構建一個 f(x) 的函數。若要計算 a, b, c, d 各自的函數值，對於傳統電腦來說，就是一個一個代入計算：

f(a), f(b), f(c), f(d)

但在量子的世界，可以讓一個或多個量子位元處於疊加態：

|a⟩+|b⟩ + |c⟩+|d⟩

然後將這個疊加態輸入設計好的 f(x) 邏輯閘做平行運算，得到：

|f(a)⟩+|f(b)⟩ + |f(c)⟩+|f(d)⟩

到這邊還需要先知道另一個 Shor’s Algorithm 的核心概念。一樣目標是找到滿足條件的 p。如果現在隨便找的一個 x，會得到 g^x = mN + r，其中 r 是餘數，那麼很容易證明 g^x + p = m₂N + r 也成立。

換句話說，對於某個週期 p，g^x 模 N 的餘數會重複出現：

g^x mod N = r ⟹ g^x + p mod N = r

這個「週期性」就是 Shor’s Algorithm 能有效率分解質因數的關鍵。只要能找到這個週期 p，就能透過 Quantum Fourier Transform（量子傅立葉變換）進一步拆解 N。

前面提到，在量子的世界中，我們可以構建量子閘，讓所有輸入 x 的餘數 r 同時被計算出來：

|x⟩→|x⟩|g^x mod N⟩

這表示，當量子位元處於疊加態時，經過適當設計的量子閘後，所有 x 對應的 g^x mod N 都會同時存在於量子態中。

從這些餘數當中，任取一個 r，可以經由適當的轉換，將其餘的 x 都變成 0。最後透過 Fourier Transform 找出的 g = x 和 p，就可以利用前面提過的傳統方式，判斷 g^p/2 ± 1 是否與 N 有公因數，將 N 拆解開來。

標準的 2048 位元 RSA 加密，就算用目前世界上最強的超級電腦（太湖之光，中國製），花費地球年齡的時間（46 億年）都無法破解。

如果量子電腦真的存在，能將運算時間由數十億年縮減為幾分、幾秒鐘，數字 N 都能快速被拆解成 f₁, f₂ 兩個質數，現在的金融、通訊等都會受到嚴重的影響。但是現在還不需要擔心，因為目前的技術還沒辦法處理太多位元的數字，可能只能拆解 15 = 3 × 5 這種容易的而已。

單量子位系統 (Single-Qubit Quantum Systems)

在量子計算中，量子位元 (Qubit) 是最基本的資訊單位，類似於傳統計算中的位元 (Bit)。然而，與傳統位元只能處於 0 或 1 的狀態不同，量子位元可以同時處於 0 和 1 的疊加態。先來介紹一下量子計算所處於的空間定義：

Hilbert 空間 (Hilbert Space)

對於單量子位元系統，Hilbert 空間是一個複數 ℂ 中的 inner product space，有向量加法、純量乘法，以及計算向量之間的內積。

If |ψ⟩,|ϕ⟩ ∈ V, α, β ∈ ℂ, then α|ψ⟩+β|ϕ⟩ ∈ V.

在單量子位元系統當中，我們常用, 當作標準基底，而一個量子位元則可表示為 |ψ⟩=α|0⟩ + β|1⟩。

至於維度 (Dimension) 為 N 的向量空間，則會以 {|e₁⟩,|e₂⟩, …, |e_N⟩} 當作標準基底，也可以寫成{|0⟩,|1⟩, …, |N − 1⟩} 。

正規化 (Normalized)：⟨e₁|e₁⟩=⟨e₂|e₂⟩ = … = ⟨e_N|e_N⟩ = 1
正交 (Orthogoral)：⟨e₁|e₂⟩=⟨e₂|e₃⟩ = … = ⟨e_N − 1|e_N⟩ = 0

因此：

Note：單量子位元系統的 Hilbert 空間是一個 N = 2 的簡單空間，而複數量子位元系統的 Hilbert 空間維度會隨著量子位元數量增加而指數成長，例如 n = 5 個量子位元系統的 Hilbert 空間維度為 N = 2⁵ = 32。

範例

我們拿一個例子來說明好了，假設 , ，那麼可以做下列這幾個運算：

對偶向量 (Dual Vector)

內積 (Inner Product)

因此：

⟨v|v⟩ ∈ ℝ_≥ 0 (non-negative real)
(a⟨v₂|+b⟨v₃|)|v₁⟩=a⟨v₂|v₁⟩ + b⟨v₃|v₁⟩

向量範數 (Norm)

正規化向量 (Normalized Vector)

量子態必須是正規化的，以保證測量結果的機率總和為 1。

例如：

計算內積：

投影運算子 (Projection Operator)

此時算出的和就分別是 |ψ⟩ 在 |e₁⟩ 和 |e₂⟩ 兩個基底的投影運算子。

崩塌 (Collapse)

我們前面說過，|ψ⟩=∑_iα_i|e_i⟩ 是由N維的基底所組成的。其中 |e_i⟩ 在 |ψ⟩ 出現的機率為 |α_i|²，則|α₁|² + |α₂|² + … + |α_N|² = 1。

範例

|e₁⟩ 在 |ψ⟩ 出現的機率為
|e₂⟩ 在 |ψ⟩ 出現的機率為

量子態 (Quantum State)：

P_i|ψ⟩→|e_i⟩

|ψ⟩=α₁|e₁⟩ + α₂|e₂⟩

經典態 (Classical State)：

量子態在測量後會崩塌到某個基底態，而此時的經典態不再具有量子態的疊加性。

Bloch 球 (Bloch Sphere)

Bloch 球用於表示單量子位的狀態：video

|0⟩ → (0,0,1)
|1⟩ → (0,0,−1)
| + ⟩ → (1,0,0)
| − ⟩ → (−1,0,0)
|i⟩ → (0,1,0)
| − i⟩ → (0,−1,0)

Bloch 球上的 I, X, Y, Z 運算子幾何意義

I (單位運算子)：不改變 Bloch 球上的狀態（即不旋轉）。
X 門（Pauli-X）：繞 x 軸旋轉 π 弧度（180°），將 |0⟩ 和 |1⟩ 互換。對應於 Bloch 球上的 x 軸翻轉。
Y 門（Pauli-Y）：繞 y 軸旋轉 π 弧度（180°），將 |0⟩ 和 |1⟩ 互換，並帶有相位。對應於 Bloch 球上的 y 軸翻轉。
Z 門（Pauli-Z）：繞 z 軸旋轉 π 弧度（180°），將 | + ⟩ 和 | − ⟩ 互換，|0⟩ 不變，|1⟩ 變號。對應於 Bloch 球上的 z 軸翻轉。

簡單來說，X, Y, Z 分別對應於 Bloch 球上繞 x、y、z 軸的 180° 旋轉。

多量子位系統 (Multiple-Qubit Systems)

Hilbert 空間與張量積 (Tensor Product)

多量子位系統的 Hilbert 空間是單量子位空間的張量積：

H₂ ⊗ H₂ ⊗ … ⊗ H₂ = H_N (N 個)

假設：

第 0 個 H₂：{|0⟩₀,|1⟩₀}
第 1 個 H₂：{|0⟩₁,|1⟩₁}

Tensor Product

H₂ ⊗ H₂:

|ψ₁⟩⊗|ψ₀⟩ = [α₁|0⟩₁+β₁|1⟩₁] ⊗ [α₀|0⟩₀+β₀|1⟩₀]

= α₁α₀|0⟩₁⊗|0⟩₀ + α₁β₀|0⟩₁⊗|1⟩₀ + β₁α₀|1⟩₁⊗|0⟩₀ + β₁β₀|1⟩₁⊗|1⟩₀

= α₁α₀|00⟩₁₀+α₁β₀|01⟩₁₀ + β₁α₀|10⟩₁₀+β₁β₀|11⟩₁₀

而此時：

|0⟩₁⊗|0⟩₀ = |00⟩₁₀
|0⟩₁⊗|1⟩₀ = |01⟩₁₀
|1⟩₁⊗|0⟩₀ = |10⟩₁₀
|1⟩₁⊗|1⟩₀ = |11⟩₁₀

|00⟩,|01⟩, |10⟩,|11⟩ 為 H₄ 的基底

範例

假設：

第 0 個 H₂：, , T₀ operator
第 1 個 H₂：, , T₁ operator

計算張量積：

運算子與單元矩陣

在多量子位系統中，運算子 T 和單位運算子 I 的結合可以用來描述量子態的演化。假設 T₀ 和 T₁ 是作用於不同量子位的運算子，若它們相等，即 T₀ = T₁ = T，則可以簡化為單一運算子 T 的作用。

單位運算子 I 的作用不會改變量子態，滿足以下關係：

I|ψ⟩=|ψ⟩

其中，單位運算子 I 的矩陣形式為：

當運算子 T 作用於單一量子位的量子態時，可以表示為：

T|ψ₁⟩,|ψ₀⟩

而當運算子 T 與單位運算子 I 結合，作用於多量子位系統的張量積態時，則可以表示為：

(T⊗I)(|ψ₁⟩⊗|ψ₀⟩)

單位運算子：

單元矩陣 (Unitary Matrix)

假設 U ：

則可發現 U⁻¹ = U^†

Note：共軛轉置 (conjugate) U^† = (U^*)^T

U 是 Unitary Matrix

量子門與狀態轉換 (Quantum Gates and State Transformations)

常見量子門

H₂ 的基本運算子為 I, X, Y, Z

基本運算子 - X (NOT)

X|0⟩=|1⟩, X|1⟩=|0⟩

其中：

X² = I = X⁻¹X

X⁻¹ = X

基本運算子 - Y

Y|0⟩=+i|1⟩, Y|1⟩=−i|0⟩

其中：

Y^† = Y

Y² = I

Y 是單元矩陣

基本運算子 - Z

Z|0⟩=|0⟩, Z|1⟩=−|1⟩

糾纏態與測量

在H₂中，

U = αI + βX + γY + δZ

Bell State （貝爾態）

Bell State 是兩個 qubit 之間最純粹的糾纏態。

假設：

|ψ₁⟩=α₁|0⟩ + β₁|1⟩, |ψ₀⟩ = α₀|0⟩+β₀|1⟩

則它們的張量積

|ψ₁⟩⊗|ψ₀⟩ = α₁α₀|00⟩+α₁β₀|01⟩ + β₁α₀|10⟩+β₁β₀|11⟩

如果 β₁α₀ = α₁β₀ = 0，則為 可分離態；否則為 糾纏態 (entanglement)。

糾纏測量

α₁α₀|00⟩+β₁β₀|11⟩ ≠ |ψ₁⟩⊗|ψ₀⟩

例如：

|00⟩+|11⟩ = |0⟩₁⊗|0⟩₀ + |1⟩₁⊗|1⟩₀

此時去做量子測量：

第 1 個質點測量到 |0⟩，則第 0 個質點就確定為 |0⟩
第 1 個質點測量到 |1⟩，則第 0 個質點就確定為 |1⟩

逆向計算 (Reverse Computation)

CNOT (Control NOT)

CNOT 門的運作如下：

CNOT 性質：

CNOT ⋅ CNOT = I

CNOT⁻¹ ⋅ CNOT = I

CNOT⁻¹ = CNOT

舉個例子：

1 ⊗ 0 = 1	1 ⊗ 1 = 0

這是所有計算中最重要的一個運算門，並且可以延伸出 COPY、NOT 和 SWAP 三種操作：

COPY	NOT	SWAP

CCNOT (Toffoli Gate)

CCNOT 門的運作如下：

a = 0, b = 0 ⟹ ab = 0 ⟹ |c⊕ab⟩=|c ⊕ 0⟩ = |c⟩

CCNOT 性質：

CCNOT ⋅ CCNOT = I

CCNOT⁻¹ ⋅ CCNOT = I

CCNOT⁻¹ = CCNOT

邏輯運算門

AND

AND 的運作如下：

XOR

XOR 的運作如下：

NAND (NOT AND)

NAND 的運作如下：

NOT

NOT 也可以用 CNOT 的形式來表示：

OR

OR 的運作如下：

範例

以下是量子電路的等價性：